书接上文。
Chapter 3:光线,相机和背景
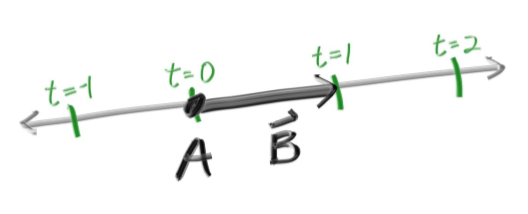
所有光线追踪器都应该有的是ray类,可以计算出沿着这个光线上可以看到的颜色。让我们把光线视为一个函数:p(t) = A + t * B
p是3D空间下的一条直线上的点,A是线的起点,B是光线的方向。t则是实际的参数(代码中是float类型)。插入不同的t,p(t)会在光线上移动。加入负数的话,可以得到3D直线的任意位置(反方向的延长线上)。正数的t则是在A点的前方,这被称作 half-line(半光线)或者光线。
下面是ray类的代码:
#ifndef RAYH
#define RAYH
#include "vec3.h"
class ray
{
public:
ray(){}
ray(const vec3& a, const vec3& b) { A = a; B = b; }
vec3 origin() const { return A; }
vec3 direction() const { return B; }
vec3 point_at_parameter(float t) const { return A + t*B; }
vec3 A;
vec3 B;
};
现在我们准备来写光线追踪器。光追器的核心就是发射光线穿过像素点,计算这些方向的光线上的颜色。另一种形式是计算从眼睛到像素的光线,计算相交的光线,和相交点的颜色。(没懂这说的啥)当第一次开发一个光追器,我常常做个简单的摄像机来把代码跑起来。我也会做一个简单的color函数来得到背景的颜色。
由于我经常搞混x和y,使用方形图片来debug常常使我陷入麻烦,所以我坚持用200*100的图片,并且会把“眼睛”(或者相机中心,如果你把它想象成相机的话)放在(0,0,0)的位置。把y轴向上,x轴向右。为了满足右手坐标系,向着屏幕的方向是z轴的负方向。同样我从左下角作为屏幕的原点(大意。。。)并且使用两个偏移向量。。。。(没懂)。注意我并没有使用单位向量,因为我觉得这么做更简单更快。
在下面的代码中,光线r近似的穿过像素的中心(我并不担心精确性的问题,之后我会添加抗锯齿):
#include "stdafx.h"
#include <iostream>
#include <fstream>
#include "vec3.h"
#include "ray.h"
using namespace std;
vec3 color(const ray& r)
{
vec3 unit_direction = unit_vector(r.direction());
float t = 0.5*(unit_direction.y() + 1.0);
return (1.0 - t)*vec3(1.0, 1.0, 1.0) + t*vec3(0.5, 0.7, 1.0);
}
int main()
{
ofstream outfile("chapter3_ray_output.ppm", ios_base::out);
int nx = 200;
int ny = 100;
outfile << "P3\n" << nx << " " << ny << "\n255\n";
vec3 lower_left_corner(-2.0, -1.0, -1.0);
vec3 horizontal(4.0, 0.0, 0.0);
vec3 vertical(0.0, 2.0, 0.0);
vec3 origin(0.0, 0.0, 0.0);
for (int i = ny - 1; i >= 0; i--)
{
for (int j = 0; j < nx; j++)
{
float u = float(j) / float(nx);
float v = float(i) / float(ny);
ray r(origin, lower_left_corner + u*horizontal + v*vertical);
vec3 col = color(r);
int ir = int(255.99 * col[0]);
int ig = int(255.99 * col[1]);
int ib = int(255.99 * col[2]);
outfile << ir << " " << ig << " " << ib << "\n";
}
}
return 0;
}
这个光线函数基于y坐标线性混合白色和蓝色。一开始我得到了(-1,1)范围内的单位向量,之后我缩放到(0,1)范围内。当t=1时我希望是蓝色,t=0是白色,中间则是混合。这形成了线性混合或者线性插值,或者简单的说插值(lerp)。插值的形式:blended_value = (1 - t) * start_value + t * end_value,t的取值范围是(0,1)。我们的例子里结果是:

Chapter4:添加球体
在光追器里加个简单的物体。人们常常使用球体,因为计算光线是不是击中了球体非常的简单直接。球心在原点的球的公式是:x*x + y*y + z*z = R*R,换句话说“对于任何(x,y,z)点,如果x*x + y*y + z*z = R*R,那么(x,y,z)点在球面上”。但是如果球心在(cx,cy,cz)处的话,公式就会变得很丑:
(x−cx)*(x−cx) + (y−cy)*(y−cy) + (z−cz)*(z−cz)=R*R
由于向量的关系,你总是希望在图形学的所有的公式中的x/y/z都转化成vec3类。你可能意识到了从球心C到点p的向量可以表示成(p-C)。并且
dot(p−C,p−C)=(x−cx)*(x−cx) + (y−cy)*(y−cy) + (z−cz)*(z−cz)
所以公式又可以表达成
dot((p − c),(p − c)) = R*R
我们可以把它看作“所以满足等式的点都在球面上”。我们想要知道光线p(t) = A + t*B是否击中了球面的某个地方。如果它击中了球体,那么一定有t存在满足球的等式。所以我们找到有t存在当等式成立即可:
dot((p(t) − c),(p(t) − c)) = R*R
可以通过光的函数展开:
dot((A + t*B − C),(A + t*B − C)) = R*R
等式变换:
t∗t∗dot(B,B) + 2∗t∗dot(A−C,B) + dot(A−C,A−C) − R∗R = 0
PS:之前在CSDN上下载的版本这里居然是
t∗t∗dot(B,B) + 2∗t∗dot(A−C,A−C) + dot(C,C) − R∗R = 0
感觉这个等式是错的,推算了一下应该是(看了参考网站的版本,确实是错的。。。)
PSS:后来找了作者官方发布的PDF,确实之前二手论坛(CSDN)下的是错误的版本…千万别看盗版书啊Orz
向量和R都是已知数,t是未知数,方程是二次的,就像你在高中的时候学到的那些。你可以解出t来,根据平方根的正负零值,可能会有两个实数解,一个实数解和零个实数解的情况。在图形学中,代数总能直观的表现在几何中:
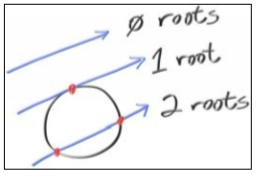
如果我们把这个硬编码到我们的程序中,放置一个在z轴-1位置的球,通过把击中球面的像素涂红,我们可以测试一下:
bool hit_sphere(const vec3& center, float radius, const ray& r)
{
vec3 oc = r.origin() - center;
float a = dot(r.direction(), r.direction());
float b = 2.0 * dot(oc, r.direction());
float c = dot(oc, oc) - radius * radius;
float discriminant = b * b - 4 * a * c;
return (discriminant > 0);
}
vec3 color(const ray& r)
{
if (hit_sphere(vec3(0, 0, -1.0), 0.5, r))
return vec3(1.0, 0, 0);
vec3 unit_direction = unit_vector(r.direction());
float t = 0.5*(unit_direction.y() + 1.0);
return (1.0 - t)*vec3(1.0, 1.0, 1.0) + t*vec3(0.5, 0.7, 1.0);
}
然后我们就得到了:

现在这个虽然缺少大量的东西——像光影,反射光等等,但我们已经接近完成一半了。一个值得注意的是我们需要测试光线是否击中了球体,但是t<0的解也显示出来了。如果你把球心放在z = +1的地方,你可以得到相同的图片,就像你看见了后面!这个可不是一个feature!(lol)我们接下来解决这个问题。
未完待续。