Ray Tracing in One Weekend - Study Note 01 - 秘境工坊

最近在学习Ray Tracing in One Week，虽然名字有点标题党，但确实是一本不可多得的好书（毕竟众多大佬推荐）。虽然关于这本书的学习资料已经有很多了，不过反正是学习笔记（翻译和一点补充），整理在自己博客里做一个记录吧。

第一本总共有13章（加概论），全放在一篇博客里看着太累，大概分成一篇两章的样子发布。

OK，开始。

Chapter 0：概论

作者简介，成书背景等等。

Chapter 1：输出第一张图片

当你开始渲染器的时候，你需要一个看见图片的方式。最直接的方式就是写进文件。关键在于（图片文件）有那么多种格式，而其中大部分都很复杂。我常用的是纯文本的ppm格式。下面Wiki的解释挺不错的：

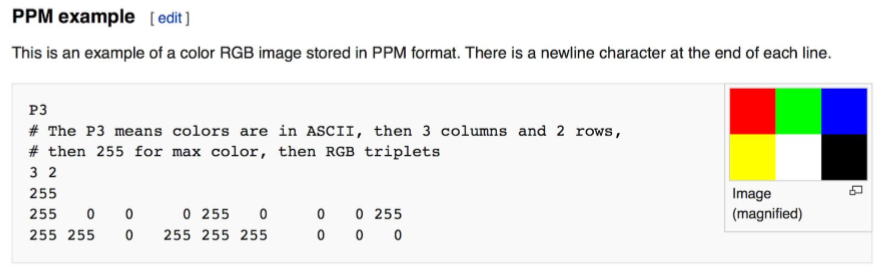
我们写点C++代码来输出些东西：

int main()
{
    int nx = 200;
    int ny = 100;
    std::cout << "P3\n" << nx << " " << ny << "\n255\n";
    for (int i = ny - 1; i >= 0; i--)
    {
        for (int j = 0; j < nx; j++)
        {
            float r = float(j) / float(nx);
            float g = float(i) / float(ny);
            float b = 0.2;
            int ir = int(255.99*r);
            int ig = int(255.99*g);
            int ib = int(255.99*b);
            std::cout << ir << " " << ig << " " << ib << "\n";
        }
    }
    return 0;
}

代码中的几个点说明一下：

每一行的像素从左到右输出
各行从上到下输出
照惯例每一个R/G/B部分的取值范围在0.0-1.0之间。我们可能会在内部使用高动态范围（译注：比如0-255），但是在输出之前我们还是会把他映射到0-1的范围，所以代码不会改变。
从左到右由黑变红，从下到上由黑变绿。红色和绿色融合成黄色，所以我们可以想见右上角是黄色的。

输出图像文件

打开输出的文件，我们可以看见：（在我的mac上使用ToyViewer打开的，你也可以用你喜欢的浏览器，如果不支持，你可以google“ppm浏览器”）

哦耶，这就是图形学版的“Hello World”。如果你的图片看起来不是这样的，用文本编辑器打开输出的文件看看，应该是像下面这样的：

如果不是，你可能加了一些行或者啥的迷惑了图片浏览器。

如果你想试试除了PPM更多的格式，试试Github上的stb_image.h，我挺喜欢的。

自注：

试了一下作者的代码，发现不能输出到文件，可以看到终端中的输出和预想差不多。。。但是说好的输出成ppm文件呢？？？
于是在网上找到了一篇文章，修改了一下代码：
https://blog.csdn.net/libing_zeng/article/details/54412618

#include "stdafx.h"
#include <iostream>
#include <fstream> // 添加 输出到文件的库
#include "vec3.h"
	 
using namespace std;
	 
int main()
{
    ofstream outfile("chapter1_output.ppm", ios_base::out); // 输出地址

    int nx = 200;
    int ny = 100;
    outfile << "P3\n" << nx << " " << ny << "\n255\n"; // 输出
    <…>
}

Chapter 2：vec3类

几乎所有的图形程序都会使用一些类来存储几何向量和颜色。在许多系统中这些向量是4D的（几何的3D加上齐次坐标，颜色的话RGB的加上透明通道）。对于我们来说，3个坐标就够了，所以我们用vec3来存储颜色，位置，方向，偏移等几乎所有的东西。也许有些人不喜欢这样，因为这不会阻止你做一些蠢事，像在位置坐标加上颜色。这很有道理，但我们这里采取“最少代码”原则，只要不是错的太离谱。

下面是vec3类的第一部分：

#ifndef VEC3H
#define VEC3H
 
#include <math.h>
#include <stdlib.h>
#include <iostream>
 
class vec3 {
 
public:
    vec3() {}
    vec3(float e0, float e1, float e2) { e[0] = e0; e[1] = e1; e[3] = e2; }
    inline float x() const { return e[0]; }
    inline float y() const { return e[1]; }
    inline float z() const { return e[2]; }
    inline float r() const { return e[0]; }
    inline float g() const { return e[1]; }
    inline float b() const { return e[2]; }
   
    inline const vec3& operator+() const { return *this; }
    inline vec3 operator-() const { return vec3(-e[0], -e[1], -e[2]); }
    inline float operator[](int i) const { return e[i]; }
    inline float& operator[](int i) { return e[i]; };
   
    inline vec3& operator+=(const vec3 &v2);
    inline vec3& operator-=(const vec3 &v2);
    inline vec3& operator*=(const vec3 &v2);
    inline vec3& operator/=(const vec3 &v2);
    inline vec3& operator*=(const float t);
    inline vec3& operator/=(const float t);
   
    inline float length() const { return sqrt(e[0] * e[0] + e[1] * e[1] + e[2] * e[2]); }
    inline float squared_length() const { return e[0] * e[0] + e[1] * e[1] + e[2] * e[2]; }
    inline void make_unit_vector();
   
    float e[3];
}; 
#endif // ! VEC3H

向量运算

我在这用了float类型，不过在其他的光线追踪器中也用double类型。并不存在正确与否——顺从你自己的品味就行。这些都是写在头文件中，接下来我们要写一些向量运算：

inline vec3 operator+(const vec3 &v1, const vec3 &v2)
{
    return vec3(v1.e[0] + v2.e[0], v1.e[1] + v2.e[1], v1.e[2] + v2.e[2]);
}
 
inline vec3 operator-(const vec3 &v1, const vec3 &v2)
{
    return vec3(v1.e[0] - v2.e[0], v1.e[1] - v2.e[1], v1.e[2] - v2.e[2]);
}
 
inline vec3 operator*(const vec3 &v1, const vec3 &v2)
{
    return vec3(v1.e[0] * v2.e[0], v1.e[1] * v2.e[1], v1.e[2] * v2.e[2]);
}
 
inline vec3 operator/(const vec3 &v1, const vec3 &v2)
{
    return vec3(v1.e[0] / v2.e[0], v1.e[1] / v2.e[1], v1.e[2] / v2.e[2]);
}

几何运算

/和*运算符是给颜色计算时使用的，你不太会想用在类似于坐标的运算中。同样，我们也有一些为几何准备的运算符：

inline float dot(const vec3 &v1, const vec3 &v2)
{
    return v1.e[0] * v2.e[0] + v1.e[1] * v2.e[1] + v1.e[2] * v2.e[2];
}
	 
inline vec3 cross(const vec3 &v1, const vec3 &v2)
{
    return vec3((v1.e[1] * v2.e[2] - v1.e[2] * v2.e[1]),
      -(v1.e[0] * v2.e[2] - v1.e[2] * v2.e[0]),
      (v1.e[0] * v2.e[1] - v1.e[1] * v2.e[0]));
}

计算单位向量

还有计算出和输入向量方向一致的单位向量：

// 似乎原文没有添加向量和浮点数的乘除法计算，计算单位向量时会报错
inline vec3 operator*(float t, const vec3 &v) 
{
    return vec3(t*v.e[0], t*v.e[1], t*v.e[2]);
}
 
inline vec3 operator/(vec3 v, float t) 
{
    return vec3(v.e[0] / t, v.e[1] / t, v.e[2] / t);
}

inline vec3 unit_vector(vec3 v) 
{
    return v / v.length();
}

使用运算方法

现在我们可以改改main中的代码，使用我们刚写的vec3类：

#include "stdafx.h"
#include <iostream>
#include "vec3.h"
 
int main()
{
    int nx = 200;
    int ny = 100;
    std::cout << "P3\n" << nx << " " << ny << "\n255\n";
    for (int i = ny - 1; i >= 0; i--)
    {
        for (int j = 0; j < nx; j++)
        { 
            // chapter 2
            vec3 col(float(i) / float(nx), float(j) / float(ny), 0.2);
            int ir = int(255.99 * col[0]);
            int ig = int(255.99 * col[1]);
            int ib = int(255.99 * col[2]);

            std::cout << ir << " " << ig << " " << ib << "\n";
        }
    }
    return 0;
}

自注：

Vec3类的文件要放在哪个文件里，也是一个问题，根据参考博客，类的定义都放在头文件中：

–	非模板类型(none-template)	模板类型(template)
头文件(.h)	全局变量申明（带`extern`限定符）全局函数的申明带inline限定符的全局函数的定义	带`inline`限定符的全局模板函数的申明和定义
–	类的定义类函数成员和数据成员的申明（在类内部）类定义内的函数定义（相当于`inline`）带`static` `const`限定符的数据成员在类内部的初始化带`inline`限定符的类定义外的函数定义	模板类的定义模板类成员的申明和定义（定义可以放在类内或者类外，类外不需要写`inline`）
实现文件(.cpp)	全局变量的定义（及初始化）全局函数的定义	(无)
–	类函数成员的定义类带`static`限定符的数据成员的初始化

未完待续。

其他笔记

参考资料：

“In One Weekend：原书博客”

“作者发布在GoogleDrive上的PDF，请尽量在Amazon购买支持”

“总结《Ray Tracing in One Weekend》 by 图形跟班”

Ray Tracing in One Weekend - Study Note 01

周末掌握光线追踪 - 学习笔记一：图像和向量类